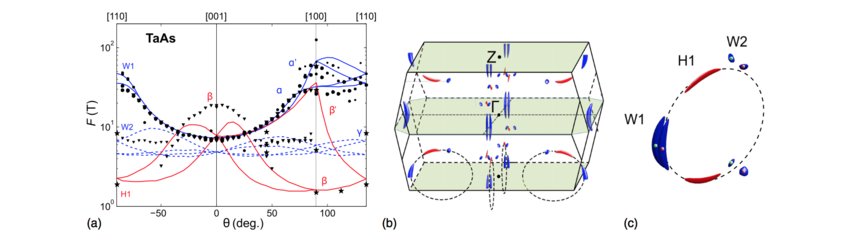
Fermi surface and transport of Weyl semimetals

Weyl semimetals are materials where valence and conduction bands cross in single points, the Weyl nodes. When the Fermi energy is near these nodes, the electrons effectively behave as relativistic Weyl fermions with a linear energy dispersion and a well-distinguished chirality.

The existence of Weyl fermions was predicted in high energy physics in 1929 but never confirmed until 2015. In that year, researchers detected the surface states originating in the topological nature of Weyl nodes by angle resolved photoemission spectroscopy. A bulk signature of Weyl fermions is predicted to be a negative magnetoresistance induced by the so-called chiral anomaly, when electric current and magnetic field are parallel. One obvious condition to observe such a Weyl fermionic behaviour is that the Fermi energy in a material has to be close to the Weyl nodes. However, it is still not clear how close and what is the influence of the distance on the bulk transport properties. Measurements of the Fermi surface via quantum oscillations combined with band-structure calculations give us information on the distance of the Fermi energy to the Weyl nodes in a given material. Experimentally, we determine the oscillations of resistivity or magnetisation in magnetic field at low temperature and this will allow a reconstruction of the Fermi surface topography of proposed Weyl semimetal candidates and give information about the effective mass and scattering. This way it can be seen in which materials the Fermi energy are close enough to the Weyl nodes so that the Fermi surface pockets contain separated Weyl nodes, which therefore have a well-defined chirality.

Tantalum arsenide is a Weyl semimetal where the electronic structure was studied profoundly and our results showed the presence of Fermi surface pockets in TaAs with separate Weyl nodes (see ref. Arnold et al., PRL117, 2016). In TaP, on the other hand, Fermi surfaces around Weyl-node pairs emerge that are not penetrated by an integer flux of Berry curvature (and are therefore topologically trivial). In NbAs however, the distance of the Weyl nodes to the Fermi energy seems to be the smallest in these compounds and it is therefore suited for further investigations of the chiral anomaly (see ref. Naumann et al, arXiv:2105.12090 ). Our latest research on TaAs investigates whether hydrostatic pressure can shift the Fermi level even closer to the Weyl nodes in this material and enables us to get experimental access to Weyl fermionic properties.

We are also interested in the behaviour of the physical properties of Weyl semimetals in a magnetic field so high that only the lowest Landau level is occupied. For this project we collaborate with the MagSup group at the Institute Néel in Grenoble, France.

Fermi surface of CoSb₃

Fig. 2 (a) Effective mass m* of the quasiparticles in CoSb3 measured via the temperature-dependent quantum oscillation amplitude (different symbols for different samples). The effective mass changes with the quantum -oscillations frequency in agreement with DFT calculations (light blue line). We also observed quantum oscillations from Sb inclusions. (b) Calculated band structure along high-symmetry directions. The Fermi level for two frequencies is indicated in red and blue. Naumann and Mokhtari et al. PRB 2021 — **Fig. 2** (a) Effective mass m* of the quasiparticles in CoSb₃ measured via the temperature-dependent quantum oscillation amplitude (different symbols for different samples). The effective mass changes with the quantum -oscillations frequency in agreement with DFT calculations (light blue line). We also observed quantum oscillations from Sb inclusions. (b) Calculated band structure along high-symmetry directions. The Fermi level for two frequencies is indicated in red and blue. Naumann and Mokhtari et al. PRB 2021

**Fig. 2** (a) Effective mass m* of the quasiparticles in CoSb₃ measured via the temperature-dependent quantum oscillation amplitude (different symbols for different samples). The effective mass changes with the quantum -oscillations frequency in agreement with DFT calculations (light blue line). We also observed quantum oscillations from Sb inclusions. (b) Calculated band structure along high-symmetry directions. The Fermi level for two frequencies is indicated in red and blue. Naumann and Mokhtari et al. PRB 2021

The unfilled skutterudite CoSb₃ is a small-gap semiconductor. Applying uniaxial strain results in a closure and a subsequent inversion of the gap. When the valence and conduction bands touch each other at a single point (node), they form a Dirac cone with a characteristic linear dispersion near the Fermi energy. This enables a study of a continuous transition from a normal semiconductor to a topologically non-trivial material across a topological quantum critical point. Our work presented here served as a starting point for strain measurements and was aimed at characterising the electronic structure of as-grown samples. Two types of samples, one grown in Sb flux and the other by an inclined rotary Bridgman technique, were compared based on structural properties, resistivity, Hall effect, and magnetisation. All samples appeared metallic with small growth-dependent hole doping. Previously, the band structure has been investigated by analysing the Shubnikov–de Haas effect, which could be observed in this material in high magnetic fields. However, these data only allowed a limited analysis due to elevated noise levels in pulsed magnetic fields and the observation of only a few oscillation periods. A detailed investigation of the electronic structure and properties and their dependence on the growth conditions was lacking.

In our work, we observed quantum oscillations in magnetisation and angle-dependent electronic transport. We studied a number of samples of both growth types. The Fermi surface consists of a single spherical sheet at the Γ point. Different samples showed slightly different doping levels, leading to various sizes of the respective Fermi surfaces, and consequently distinct periodicities of the quantum oscillations. The purest samples grown by the Bridgman technique had an oscillation frequency of 20 T corresponding to a Fermi energy lying only 25 meV below the valence-band edge. We found that samples grown by the IRB method are homogeneous, whereas signs of a sample-dependent doping level and Sb inclusions occurred in the flux-grown samples. This is reflected in the summary of the effective masses, shown in Fig. 2, which were determined from the temperature dependences of the quantum-oscillation amplitudes. Only by establishing this graph was it possible to distinguish between the quantum oscillations from CoSb₃ and those from Sb inclusions: For similar values of the quantum oscillation frequency, Sb inclusions have a lower effective mass (light-coloured symbols).

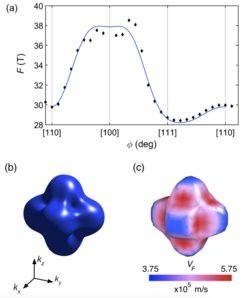
Fig. 3 Quantum-oscillation frequency versus angle in indium-doped CoSb3. (b) Fermi surface extracted from (a) agreeing very well with the largest of three Fermi surfaces from DFT calculations in (c). Naumann and Mokhtari et al. PRB 2021 — **Fig. 3** Quantum-oscillation frequency versus angle in indium-doped CoSb₃. (b) Fermi surface extracted from (a) agreeing very well with the largest of three Fermi surfaces from DFT calculations in (c). Naumann and Mokhtari et al. PRB 2021

**Fig. 3** Quantum-oscillation frequency versus angle in indium-doped CoSb₃. (b) Fermi surface extracted from (a) agreeing very well with the largest of three Fermi surfaces from DFT calculations in (c). Naumann and Mokhtari et al. PRB 2021

Furthermore, we also investigated indium substitution as a means of shifting the Fermi energy to the electron-doped region. Here, the Fermi surfaces are not spherical, leading to the angle-dependence shown in Fig. 3.

Overall, the experimental Fermi-surface properties are consistent with DFT calculations and previous experimental investigations. Therefore, we can confirm the reliability of the DFT calculations experimentally at ambient conditions in CoSb₃ for Fermi levels close to the gap. These samples and results are identified as a good starting point for future experiments under strain, where the transition to a topological insulator phase is expected.

Magnetoresistance in Weyl-semimetals

Measurements of the longitudinal magnetoresistance are highly non-trivial, when the anisotropy of the conductivity changes with magnetic field. We investigate this classical effect in the proposed Weyl semimetals and were able to show that the field concentrates the current to a narrow path through the sample in commonly used experimental conditions. We try to overcome this problem in order to determine the intrinsic longitudinal magnetoresistance in Weyl semimetals and hence detect the chiral anomaly.

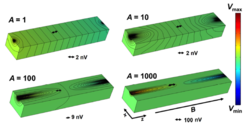
Fig. 2 Potential distribution in a bar-shaped sample for increasing conductivity anisotropy A. The current is injected in the side surface at the top middle position. The potential shows a strongly peaked structure for high A (high magnetic field). Meaningful resistance measurements have to be carried out in the limit of parallel equipotential planes (indicated by lines here). An anisotropy of A = 1000 is reached with less than 9 T in NbP. dos Reis et al., New Journal of Physics 18, 085006 (2016). — **Fig. 2** Potential distribution in a bar-shaped sample for increasing conductivity anisotropy A. The current is injected in the side surface at the top middle position. The potential shows a strongly peaked structure for high A (high magnetic field). Meaningful resistance measurements have to be carried out in the limit of parallel equipotential planes (indicated by lines here). An anisotropy of A = 1000 is reached with less than 9 T in NbP. dos Reis *et al.*, New Journal of Physics 18, 085006 (2016).

**Fig. 2** Potential distribution in a bar-shaped sample for increasing conductivity anisotropy A. The current is injected in the side surface at the top middle position. The potential shows a strongly peaked structure for high A (high magnetic field). Meaningful resistance measurements have to be carried out in the limit of parallel equipotential planes (indicated by lines here). An anisotropy of A = 1000 is reached with less than 9 T in NbP. dos Reis *et al.*, New Journal of Physics 18, 085006 (2016).

In compensated semimetals the conductivity component perpendicular to the magnetic field decreases strongly in magnetic field due to the orbital effect. On the other hand, the longitudinal conductivity (current parallel to the magnetic field) changes only slightly compared to that, so that the conductivity tensor becomes highly anisotropic in a magnetic field. As nicely explored by K. Yoshida (K. Yoshida, J. Phys. Soc. Jap. 41, 574 (1976) and later papers), this effect leads to inhomogeneous currents in the sample when the current contacts are smaller than its cross section. Fig. 2 shows the potential distribution for given values of the conductivity anisotropy A. We study this effect in the resistance and are able to show that it can lead to a decreasing apparent longitudinal magnetoresistance with field, just as expected for the chiral anomaly (see the figure at the top). This puts strong constrains on the experimental determination of the longitudinal magnetoresistance like perfect current contacts over the whole cross section of the sample and a perfect alignment of the magnetic field.

Fig. 1 Coloured lines show the longitudinal magnetoresistance of the Weyl semimetals NbAs, TaP and NbP for magnetic field B and current I along the crystallographic c-axis at T = 2 K. The chiral anomaly would lead to a negative magnetoresistance, which is not observed. Instead, the data are perfectly explained by the expected orbital magnetoresistance (dotted black lines). [Naumann et al. PRM 2021]. — **Fig. 1** Coloured lines show the longitudinal magnetoresistance of the Weyl semimetals NbAs, TaP and NbP for magnetic field B and current I along the crystallographic c-axis at T = 2 K. The chiral anomaly would lead to a negative magnetoresistance, which is not observed. Instead, the data are perfectly explained by the expected orbital magnetoresistance (dotted black lines). [Naumann et al. PRM 2021].

**Fig. 1** Coloured lines show the longitudinal magnetoresistance of the Weyl semimetals NbAs, TaP and NbP for magnetic field B and current I along the crystallographic c-axis at T = 2 K. The chiral anomaly would lead to a negative magnetoresistance, which is not observed. Instead, the data are perfectly explained by the expected orbital magnetoresistance (dotted black lines). [Naumann et al. PRM 2021].

With the aim to find evidence for the chiral anomaly, a signature of Weyl fermions, we investigated the longitudinal magnetoresistance in TaAs, TaP, NbAs and NbP by ensuring homogeneous currents. We find the intrinsic LMR to depend strongly on the crystallographic orientation of the current. The LMR along the c direction rises and saturates for fields above 4 T as depicted in Fig. 1. Using Fermi-surface geometries from band-structure calculations that had been confirmed by experiment, we show that this is the behaviour expected from a classical, purely orbital effect. The dashed lines are fits of the orbital magnetoresistance. In configurations where the orbital effect is small, i.e., for B||a in NbAs and NbP, we find a non-monotonous LMR, including regions of negative LMR. A weak-antilocalization scenario can fully account for the overall field dependence, even better than including a chiral anomaly instead. The longitudinal transport in the TaAs family can therefore be explained without including any chiral or topological effects, suggesting that their signatures are either absent or very small.

Fermi surface of CoSb3

Magnetoresistance in Weyl-semimetals

Fermi surface of CoSb₃