Fe-chalcogenide based superconductors
![Fig. 1: Temperature-pressure-composition phase diagram for the Fe1+yTe system. Symbols T, M and O mark temperatures and pressures of our XRD measurements revealing tetragonal, orthorhombic and monoclinic phases, respectively. The black data points indicate anomalies in resistivity, taken from [20] for samples Fe1.086Te. AFM and IC AFM stand for antiferromagnetic and incommensurate antiferromagnetic phase, respectively.](/2875289/original-1518447550.jpg?t=eyJ3aWR0aCI6MjQ2LCJvYmpfaWQiOjI4NzUyODl9--ce398e0fa1e735009b373d8ef5103b372c9c34e9)
Sahana Rößler*, Horst Borrmann, Ulrich Burkhardt, Wilder Carrillo-Cabrera, Deepa Kasinathan, Hans-Henning Klauss1, Cevriye Koz, Yuri Grin, Philipp Materne1, Kamal Mydeen, Michael Nicklas, Ulrich K. Rößler2, Helge Rosner, Marcus Schmidt, Walter Schnelle, Ulrich Schwarz, Oliver Stockert and Steffen Wirth*
Among the different families of Fe-based superconductors, FeCh (11-type chalcogenide, Ch = Se, Te) has the simplest crystal structure [9]. The atomic pattern belongs to the tetragonal P4/nmm space group and consists of edge-sharing FeCh4 tetrahedra, which form layers orthogonal to the c-axis. The bulk superconducting transition temperature Tc of FeSe is about 8.5 K at ambient conditions with the superconducting properties being extremely sensitive to the amount of excess Fe. For instance, it has been reported that Fe1.01Se is superconducting, however Fe1.03Se is not [10]. Intriguingly, only the superconducting Fe1.01Se undergoes a structural phase transition from a tetragonal to an orthorhombic phase at Ts = 87 K while the non-superconducting Fe1.03Se does not show a corresponding structural transition [11]. Tc can become as high as 37 K by the application of hydrostatic pressure [12, 13]. This makes FeSe a member of the high-Tc class of superconductors. The antiferromagnetic fluctuations are found to be strongly increased near Tc, and applied pressure seems to enhance the spin fluctuations as well as the superconducting transition temperature. In addition, Tc of FeSe can also be increased by Te substitution of Se, up to a maximum of Tc = 15 K for Fe1+ySe0.5Te0.5 [14–16]. The bulk superconductivity disappears for higher Te substitution and no superconductivity has been found so far in bulk samples of the end-member Fe1+yTe.
Fe1+yTe is a non-stoichiometric compound which orders antiferromagnetically at low temperatures. Initial studies revealed that the structural and magnetic properties are extremely sensitive to the chemical composition. The PbO-type tetragonal crystal structure of the Fe1+yCh phases accommodate excess Fe within the crystallographic 2c sites [17]. Theoretical studies focusing on Fe1+yTe suggest a +1 valence state with a relatively large local moment of 2.4 μB for the interstitial Fe [18]. These interstitial moments are expected to couple magnetically to the moments of the Fe square substructure resulting in a complex magnetic order. Therefore, it is highly important to establish the homogeneity range of these binary chalcogenides and to determine their structure-property correlations.
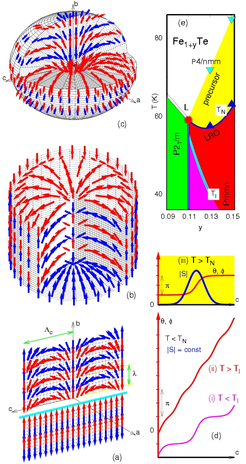

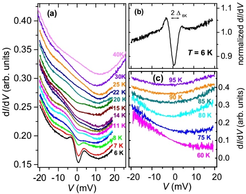
Fig. 4: (a) Raw tunneling spectra in the temperature range 6 - 40 K. (b) Normalized tunneling spectra in the temperature range 6 - 30 K. The yellow shaded region represents the energy scale of T0. (c) Raw tunneling spectra in the temperature range 60 - 95 K. The spectra are shifted vertically for clarity. For all the spectroscopy measurements, Vg = 0.02 V and Isp = 0.6 nA before opening the STM feedback loop. The bias modulation amplitude was set to 0.1 mVrms.
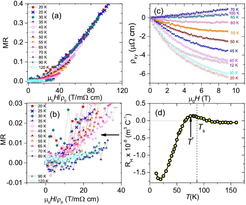
Fig. 5: (a) Kohler plot in the temperature range 20-120 K displaying the validity of Kohler’s scaling below 30 K and above 70 K. (b) Same data as shown in panel (a), but on an enlarged scale. The horizontal arrow is placed to emphasize that T* is different from Ts. (c) Hall resistivity rxy in the temperature range 12-100 K. (d) The temperature dependence of the initial Hall coefficient RH®0 displays a clear deviation from the compensated metal regime below T* ≈ 75 K where spin fluctuations become important.
![Fig. 1: Temperature-pressure-composition phase diagram for the Fe1+yTe system. Symbols T, M and O mark temperatures and pressures of our XRD measurements revealing tetragonal, orthorhombic and monoclinic phases, respectively. The black data points indicate anomalies in resistivity, taken from [20] for samples Fe1.086Te. AFM and IC AFM stand for antiferromagnetic and incommensurate antiferromagnetic phase, respectively. Fig. 1: Temperature-pressure-composition phase diagram for the Fe1+yTe system. Symbols T, M and O mark temperatures and pressures of our XRD measurements revealing tetragonal, orthorhombic and monoclinic phases, respectively. The black data points indicate anomalies in resistivity, taken from [20] for samples Fe1.086Te. AFM and IC AFM stand for antiferromagnetic and incommensurate antiferromagnetic phase, respectively.](/2875289/original-1518447550.jpg?t=eyJ3aWR0aCI6ODQ4LCJmaWxlX2V4dGVuc2lvbiI6ImpwZyIsIm9ial9pZCI6Mjg3NTI4OX0%3D--908cbba8beafeb0640d552baaaa92129ae4c43d8)



