Large exchange bias in tetragonal compensated ferrimagnets. By following the rules of the chemical and magnetic ordering in Heusler materials, we have realized the compensated ferrimagnet (of approximately Mn2.6Pt0.4Ga composition) by substituting Mn to Pt in Mn3Ga tetragonal ferrimagnet [1]. Since the whole Mn3-xPtxGa (0<x<1) series exhibit a tetragonal structure, the presence of the non-zero magnetorystalline anisotropy together with segregation of the deffect ferromagnetic phase into the grains with a small characteristic volume δV and large magnetization M, results into a huge exchange-bias field HEB~(J·S)/(M·δV+Mres) of several Tesla, where J - is the effective surface exchange coupling between the compensated host phase with the residual magnetization Mres and the ferromagnetic grains with the magnetization M, S - surface of the coupling area. The fit of the experimental data, based on this formula using the calculated magnetization Mres(x) as a function of Pt content x is shown in FIG.1.
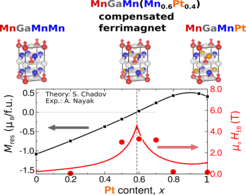
Such systems might provide an alternative appoach to the magnetic harderning. In this case the M×H product will be maximized by increasing HEB parameter. Further disorder engineering to maximize the coupling surface area S migh allow to increase the size of the ferromagnetic grains, and thus the magnetization M as well.
Noncollinear magnetism in Heusler materials. Antiparallel alignment of the magnetic moments in two different Mn sublattices is typically encountered in Mn2YZ compounds (cubic or tetragonal) but not all of them exhibit noncollinearity. The most significant exchange coupling between the nearest MnI and MnII atoms in different Wyckoff sites is characterized by a large exchange constant (JI-II∼−20 meV) that leads to a typical collinear ferrimagnetic state. However, we have identified several systematic cases (e.g., the tetragonal Mn2RhSn, Mn2PtIn and Mn2IrIn), in which the collinear ferrimagnetic order cannot explain the measured saturated magnetization, which appears to be two high. For this systems we figured out that their collinear order can be perturbed by the next important interaction j between the next-nearest planes, e.g., between pairs of MnII-Y planes, as shown in FIG.2. This interaction is antiparallel due to its indirect origin realized through the main-group element Z (superexchange). Since j tends to rotate the moments of the nearest MnII-Y planes antiparallel to each other, it competes with the strong antiparallel exchange J and may then result in a nontrivial canting angle (θ≠0°;180°). The relevant θ-dependent part of the Heisenberg Hamiltonian contains only two types of antiparallel interactions H(θ)=−J·cosθ−½·j·cos2(π−θ), where the first term is the coupling of the nearest planes (MnI-Z with MnII-Y) and the second is that of the next-nearest (MnII-Y) planes. The extrema of H(θ), θ1,2=180°±arccos(J/2j) correspond to a noncollinear solution for j > ½·J, i.e. canting occurs only if the next-nearest antiparallel exchange j is sufficiently strong. Parameterized by the ab-intio calculated J and j exchange constants, this model reasonably describes the θ-dependence of the total energy, also computed ab-initio. For Mn2RhSn, the plot of the total energy as a function of θ (FIG.2) indeed exhibits two energy minima corresponding to the nontrivial canting angles θ1,2=180°±55°, which was confirmed by neutron diffraction (θ1,2=180° ± 58.9°) [2]. Similar plots were obtained for Mn2PtIn and Mn2IrIn.

The influence of the magnetocrystalline anisotropy is figured out by rotating the easy axis of magnetization as well with the plane of the canting moments, as shown in FIG.2. In agreement with neutron data, it follows that the easy axis in Mn2RhSn coincides with the tetragonal c-axis, and the magnetocrystalline anisotropy energy is close to 2 meV/f.u. Further analysis of the micromagnetic model based on the computed Dzyaloshinski-Moriya interactions suggests the possibility for existance of the chiral skyrmions (see the supplemental in [2]).

