Discovery of new fermions in topological chiral crystals
Chiral topology is the new frontier in the field of quantum matter. In the recent study, scientists from the Max Planck Institute for Chemical Physics of Solids in Dresden discovered new fermions beyond the concept of the conventional Weyl, Dirac or Majorana fermions in chiral crystals. The new findings promises vast opportunities for future quantum applications.
An object is defined as being chiral if it cannot be superimposed by its mirror image. A very familiar example is the human hand. No-matter how one orients one’s hands, it is impossible to superimpose their major features. Such a chiral asymmetry is highly important in several branches of science, ranging from molecular chemistry to biology to physics. Recently, chirality has become a hot topic in condensed matter physics through the field of topology.
In the solid state the atoms of a chiral material follow an imaginary spiral staircase like pattern. While the staircase rotates clockwise in one system, it runs counter-clockwise in the counterpart system. However, these systems, termed “enantiomers”, are mirror images of one another. The Max Planck Institute for Chemical Physics of Solids (MPI CPfS), in Dresden, Germany, is recognized world-wide as a unique source of high quality single crystals for research into quantum applications and beyond. High quality single crystals are critical to studies of many quantum properties. In recent investigations[1,2] scientists from Claudia Felser’s group at the MPI CPfS, in collaboration with M. Zahid Hasan’s team from Princeton [1] and Niels Schroeter from PSI together with Yulin Chen’s team from Oxford [2], have investigated novel topological surface states that emerge as a consequence of the structural chirality in a particular class of chiral materials that have a P213 (198) space group (SG). The researchers have discovered a new kind of quasiparticle, the so-called Rarita-Schwinger fermions, in chiral crystals, which go beyond the known Dirac and Weyl fermions.
In conventional Weyl and Dirac semimetals quasiparticle excitations are described by the Weyl and Dirac equations, respectively, which originate from the entirely different field of high-energy physics. However, in the topological chiral crystals, the quasiparticle excitations have no corresponding analogy in high-energy physics and are therefore described as ‘New fermions’ [3]. Most remarkably, these ‘New fermions’ carry a topological charge of Chern number 4, which is four times larger than the conventional Weyl fermions. This leads to several remarkable properties that include: a giant quantized circular photo-galvanic current, a chiral magnetic effect and other novel transport and optical effects, which are forbidden in conventional topological conductors, such as the TaAs family of compounds [4].
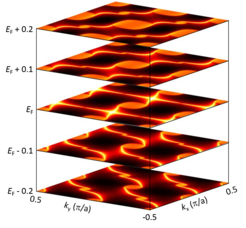
Three candidate materials were selected from the large family of binary chiral 198 SG for angle-resolved photoemission spectroscopy (ARPES) studies, namely, RhSi, CoSi [1] and AlPt [2]. The Fermi surface of these compounds is less crowded with trivial bands. ARPES experiments reveal multiple band degeneracies, or ‘New fermions’ in these chiral systems at the high symmetric points of the Brillouin zone. While the Γ point multiplet is four-fold degenerate, the R point node is six-fold degenerate. The electrons on the surface of these crystals exhibit a highly unusual helicoid structure that spirals around the two high-symmetry momenta. The complex band topology results in the longest possible Fermi arcs, which are orders of magnitude larger and more robust than any known Weyl semimetals. These investigations find the largest possible topologically nontrivial energy windows in these chiral crystals. In addition, recent investigations, already show that these materials are ideal candidates for inducing chiral magnetic effects or to observe room temperature quantized photogalvanic effects [5], suitable for future quantum applications.
[1] D. S. Sanchez et al., Nature 567, 500 (2019).
[2] N. B. M. Schröter et al., Nature Physics (2019).
[3] B. Bradlyn, J. Cano, Z. Wang, M. G. Vergniory, C. Felser, R. J. Cava, and B. A. Bernevig, Science 353, aaf5037 (2016).
[4] L. X. Yang et al., Nature Physics 11, 728 (2015).
[5] D. Rees, K. Manna, B. Lu, T. Morimoto, H. Borrmann, C. Felser, J. E. Moore, D. H. Torchinsky, and J. Orenstein, arXiv:1902.03230 (2019).