Cu(II)-Verbindungen im Zusammenspiel von Kristallchemie und Magnetismus

Seit den Anfängen der Quantenmechanik und der Entwicklung von magnetischen Wechselwirkungsmodellen im Festkörper gibt es großes Interesse an realen niedrigdimensionalen magnetischen Systemen. Trotz ihrer scheinbaren Einfachheit haben selbst einfache Modelle wie das Ising- oder das Heisenbergmodell keine exakten Lösungen für den Grundzustand, außer in ein-(1D) oder zwei-(2D) dimensionalen Systemen. Die Suche nach realen Materialien mit im Wesentlichen 1D oder 2D magnetischen Wechselwirkungen hat deshalb große Bedeutung für die Bestätigung oder Korrektur theoretischer Vorhersagen von exotischen Grundzuständen, die mit starken Quantenfluktuationen einhergehen. Hinzu kommt ein weiterer, praktischer Aspekt durch eine mögliche Schlüsselrolle solcher Quanten-Spinfluktuationen für die unkonventionelle Paarbildung in einigen Supraleitern, insbesondere den Cuprat-Hochtemperatursupraleitern.

Solche niedrigdimensionalen magnetische Materialien finden sich unter anderem in Kupfer(II)-Sauerstoff-Verbindungen, in denen quadratisch-planare CuO₄-Einheiten das strukturbildende Element sind. Die Valenzelektronenkonfiguration von Cu²⁺ entspricht 3d⁹4s⁰, die von O^2– 2p⁶. In einer einfachen Molekularfeldnäherung ist das höchste besetzte Orbital daher ein antibindender, halbgefüllter pd-σ Zustand. Aufgrund starker intraatomarer Korrelationen in den lokalisierten Cu 3d- Orbitalen ist eine solche einfache Molekularfeldbeschreibung ungenügend für die elektronischen Eigenschaften. Der halbgefüllte antibindende Zustand spaltet in ein so genanntes oberes und ein unteres Hubbard-Niveau. Somit sind die starken Korrelationen für den isolierenden Charakter der undotierten Cuprate verantwortlich. Die CuO₄-Einheit besitzt ein magnetische Moment mit dem Spin 1/2 und ist damit ein ideales Objekt, um die oben erwähnten Quanteneffekte zu studieren.

Die strukturelle und magnetische Vielfalt der Cupratverbindungen entsteht durch die Möglichkeit, die CuO₄-Basiseinheiten wie Steine aus einem Baukasten auf verschiedene Arten zu verknüpfen [1]. Auf diese Weise erhält man immer komplexere Netzwerke mit einer verblüffenden Vielfalt magnetischer Grundzustände. Unverknüpfte CuO₄-Einheiten (Abb. 1a) kann man in Verbindungen mit komplexen Anionen wie Sulfat- oder Phosphatgruppen wie zum Beispiel in den Kristallstrukturen von CuPbSO₄(OH)₂ und Sr₂Cu(PO₄)₂ (Abb. 2) finden. In anderen Verbindungen teilen sich die CuO₄-Quadrate gemeinsame Sauerstoffatome und bilden verschiedene niederdimensionale Strukturelemente (Abb. 1b-d). In Abhängigkeit von der Anzahl der gemeinsamen Sauerstoffatome entstehen so eckenverknüpfte- (Abb. 1b), kantenverknüpfte- (Abb. 1c) oder Doppel-Ketten (Abb. 1d). Durch die Kombination dieser Kettentypen kann eine große Vielfalt von Strukturen, beispielsweise ein-, zwei- oder dreibeinige Spin-Leitern gebildet werden. Auf diese Weise ist ein quasi-kontinuierlicher Übergang von 1D zu 2D Cu(II)-Verbindungen möglich.

Um die wesentlichen elektronischen und magnetischen Eigenschaften realer Verbindungen mikroskopisch zu beschreiben, sind Dichtefunktionalrechnungen (DFT) ein wertvolles Hilfsmittel. Aus der berechneten elektronischen Struktur können die wichtigsten Wechselwirkungen und die beteiligten Orbitale mithilfe eines tight-binding (TB) Modells bestimmt werden. Anschließend wird ein solches TB-Modell stufenweise auf ein Heisenberg-Modell abgebildet, um die starken elektronischen Korrelation an den Cu-Atomen möglichst realistisch zu berücksichtigen. Aus den Näherungslösungen solcher Modelle kannn man den magnetischen Grundzustand und seine Anregungen bestimmen. Dieses Verfahren wird im Folgenden stellvertretend am Beispiel von Sr₂Cu(PO₄)₂ erläutert [2].

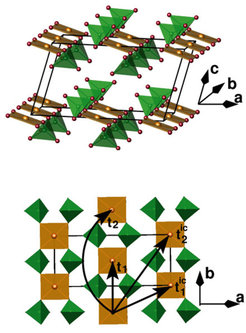
Sr₂Cu(PO₄)₂ und die isotype Verbindung Ba₂Cu(PO₄)₂ zeigen eine unter den bekannten quasi-1D-Kettenverbindungen einmalige Kristallstruktur (Abb. 2): ebene CuO₄-Quadrate sind voneinander isoliert und durch PO₄-Tetraeder zu unendlichen Ketten verknüpft. Nächste Nachbarquadrate (NN) liegen in einer Ebene, die Ketten verlaufen entlang b. CuO₄-Quadrate benachbarter Ketten entlang a besetzen die Positionen zwischen den Quadraten der Nachbarketten. Unter Berücksichtigung der strukturellen Details ist die Verbindung Sr₂Cu(PO₄)₂ am besten als Phosphato-Cuprat(II) mit einer partiellen anionischen Struktur [Cu(PO₄)₂]⁴⁺ charakterisiert.

DFT-Bandstrukturrechnungen unter Verwendung eines full-potential local-orbital (FPLO) Codes [3] finden in Übereinstimmung mit dem eingangs erläuterten Molekularfeldbild ein antibindendes, halbgefülltes Cu-O-Band an der Fermienergie und somit metallisches Verhalten. Nur das Hinzufügen der starken elektronischen Korrelationen führt zu dem isolierenden Zustand, der experimentell beobachtet wird. Eine quantitative Analyse der berechneten Bandstruktur im Rahmen eines TB-Modells offenbart den nahezu idealen 1D-Charakter der Elektronenstruktur. Zunächst zeigt sich, dass bereits die Berücksichtigung weniger, kurzreichweitiger Kopplungen (Abb. 2) genügt, um eine perfekte Übereinstimmung zwischen DFT-Bandstruktur und TB-Modell zu erzielen. Dabei findet die dominierende magnetische Kopplung zwischen Nachbarquadraten entlang einer Kette statt, alle anderen Kopplungen erweisen sich als um zwei bis drei Größenordnungen kleiner. Damit avanciert Sr₂Cu(PO₄)₂ zur besten bisher bekannten 1D- Heisenberg-Spin-1/2-Kette. Trotz der beträchtlichen magnetischen Kopplung innerhalb der Kette wird für ein solches System magnetische Ordnung – wenn überhaupt – nur bei tiefsten Temperaturen erwartet. Die berechneten magnetischen Wechselwirkungen stimmen exzellent mit den experimentellen Daten überein. Magnetische Ordnung wird erst unterhalb 85 Millikelvin beobachtet. Diese Temperatur ist etwa 2000 mal kleiner als die Wechselwirkung entlang der Ketten.

Im Wechselspiel mit thermodynamischen Messungen und theoretischen Modellrechnungen wurden so eine Reihe von Cupratkettenverbindungen mikroskopisch analysiert. Dabei wurden unter anderem neue exotische Grundzustände gefunden:

(i) LiVOCuO₄, LiCu₂O₂ und NaCu₂O₂ ordnen bei tiefen Temperaturen in Form magnetischer Quanten-Spiralen. Die treibende Kraft ist dabei eine Konkurrenz der Wechselwirkung von nächsten und übernächsten Nachbarn entlang der kantenvernetzten Cupratketten [4-8].

(ii) CuTe₂O₅ besitzt auf Grund der Bildung magnetischer Dimere eine breite Lücke in den magnetischen Anregungen. Überraschenderweise werden dabei die magnetischen Dimere nicht von benachbarten Cu-Spins gebildet.

(iii) Cu₂[PO₆(CH₂)] zeigt gleichfalls ein Spingap. Obwohl die Kristallstruktur (Abb. 3) isolierte (O₂CuO₂CuO₂)-Dimere aufweisst, die durch O₃P(CH₂)PO₃-Gruppen vernetzt werden, wird das Spingap hier nicht durch Dimerenbildung, sondern durch magnetische Frustration getrieben. Darunter versteht man die Konkurrenz von Wechselwirkungen, die verschiedene magnetische Ordnungen bevorzugen.

Diese Beispiele zeigen, dass die magnetischen Eigenschaften niedrigdimensionaler Cupratverbindungen stark von Details der Kristallstruktur abhängen. Die geplante Verwendung komplexer Oxo-Anionen von Nichtmetallen (z.B. B,C,P,S...) als abstands- und richtungskontrollierende Agentien im Kristallgitter für die Koordination der CuO₄-Einheiten sollte eine große Vielfalt von Verbindungen mit faszinierenden magnetischen Eigenschaften ermöglichen. Es wird erwartet, dass sich die Kombination theoretischer Elektronenstruktur-Rechnungen, thermodynamischer Messungen und spektroskopischer Untersuchungen zusammen mit zielgerichteten kristallchemischen Aspekten zu einem mächtigen Hilfsmittel für die künftige Erforschung eines Quanten-Phasendiagramms niedrigdimensionaler Materialien entwickelt.