“Excess” electrons in LuGe
Crystal structures of intermetallic compounds often exhibit high coordination numbers, i.e., large numbers of next neighbours. Their spatial arrangement involves polyhedrons, which are connected by sharing vertices or faces. In some atomic patterns, condensation gives rise to short distances of atoms of the same type setting the stage for covalent interactions, e.g., in the crystal structure of CaGe. The atomic arrangement comprises tricapped trigonal prisms [GeCa9], which condense by sharing rectangular faces. The formation of these columns results in zigzag chains of germanium atoms. The interrelation between chemical bonding and electron count is provided by the Zintl-Klemm concept: The valence electrons of calcium are transferred to the more electronegative germanium partial structure, which results in ionic interaction between cations and anions. The two-bonded germanium atoms in the polyanion are in line with the 8-N rule according to Ca2+(2b)Ge2-.
Then, compounds like YGe [9] would imply that the germanium chains also form in presence of ‘excess’ electrons as expressed by Y3+(2b)Ge2-×1e-. However, recent quantum chemical studies on compounds La2MGe6 (M = Li, Mg, Al, Zn, Cu, Ag, Pd) and Y2PdGe6 with similar zig-zag chains disclose significant deviations from the formal 8-N picture because of additional polar-covalent interactions between the Ge-chains and the surrounding metal atoms. During this study a similar reduction of the charge transfer was found also for LaGe in which k electrons of lanthanum participate in the bonding according to La2+k(2b)Ge2-×ke-, supplemented by an interesting bonding feature in the La partial structure [unpublished results].
As corresponding germanium compounds of heavy rare-earth metals are less studied, we applied the high-pressure high-temperature technique to prepare LuGe incorporating the smallest RE metal. This phase is not established in the ambient-pressure phase diagram, but earlier experiments evidenced synthesis at extreme conditions is an efficient tool for the preparation of hitherto inaccessible intermetallic phases.
Together with the existence of LaGe in the CrB type of structure, the discovery of LuGe in the related FeB type establishes the existence of a whole range of compounds in one of the two related structures. Quantum chemical position space analysis of chemical bonding in both phases establishes a chemical role of the “excess electrons”. The situation reminds of the one in InS, which can be written according to (1b)In2+(0b)S2-. The “excess” electron of each In2+ is involved forming an In-In dumbbell (1b)In, which leads to semiconducting behaviour. The “excess” electrons of Lu and La atoms are found to form multi-atomic R4 4-atomic bonds (Figure 1), which conceptually classifies these compounds to be located at the boundary between Zintl valence compounds and “polar intermetallic phases” [1]. From a physical point of view another comparison may be useful. In RB6 compounds, the situation concerning “excess” electrons is somewhat similar, i.e. R2+(B6)2- × 1e. There may be an interesting difference between both situations, which concerns the chemical involvement of the “excess electrons”. From our position space analysis, the “excess” electrons in RB6 are less involved in polyatomic R bonding than the ones in RGe. However, in RGe compounds there seems to be a difference between the CrB and the FeB type of structure. Indications are that the CrB type of structure favours a lower amount of chemical involvement making it more favourable for correlated electron behaviour than the FeB one.
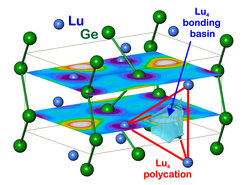
Figure 1. Multi-atomic interactions in LuGe: the distribution of the partial ELI-D calculated for the energy range -1.3 eV < E < EF in the (x¼z) and (x¾z) planes reveals the lutetium contributions to the multiatomic 4a-Lu4 bond as a structural counterpart to the chain polyanions of germanium.
FRW, US, YG












